Written by Luca Romano
Level 3, Italy

 What is a tiebreaker?

In a magic tournament, tiebreakers are those numbers with lots of decimal digits which appear in the standings of a tournament next to the name and the score of the players. They are generally infamous for making the eighth player very happy, and the ninth very sad or angry.

What is their real purpose though? Well, in a Magic tournament, the standings are defined by the score; however, because of the matchmaking system used (“Swiss round”), it’s very likely that different players can have the same score at any given time of the day. Hence the need of an additional numerical parameter, which allows to build an actual rank without having tied players.

The base principle of this parameter is the following one: if, due to some weird coincidence, you faced only mediocre opponents during the day, reaching the top would not have been that much of a deal. On the other hand, winning against strong players is more praiseworthy. The tiebreakers are indeces which measure the strenght of the players you face throughout the tournament, based on their performance during the day.

The first tiebreaker (aka “the rating” in some countries) is the percent mean of the match victories of all the opponents a player faced so far at any time of the day. At the end of the first round of Swiss, all the players with 0 points will have their first tiebreaker at 100%, since their only opponent won 100% of his/her matches.

People with 3 points should then have their first tiebreaker set to 0%, but the MTR (Magic Tournament Rules) specify that if a match-win percentage is less than 33%, it will be considered to be 33% instead. This is made to avoid negative performances of previous opponents to be too much influential: therefore, the rating of the players with 3 points at the end of round one will be 33%, the very possible minimum.

At the end of round 2, players with 6 points will have faced someone who already won round one, but they’ll have defeated him/her, so that player’s match winning percentage will be 50%. Their previous turn’s opponent could have either won or lost in the second round: in the first case the 6-point player’s first tiebreaker will be 50% (two opponents played two matches, and each one of them won one), in the second case the match-win percentage should be 0%, but we’ll be using 33% in its place: at the end of the computation the tiebreaker will be 41.5% (which is the mean between 50 and 33).

It’s intuitive that as the tournament goes on, the number of possible combinations grows exponentially. But we can also notice two important factors:

• A victory is detrimental for the first tiebreaker (of course it is beneficial for the score, which is more important): indeed, of all our opponents, one of them will have his/her match-win percentage decreased by his/her current loss. For the same reason, a loss is beneficial for the first tiebreaker.
• Losing in one of the first rounds of Swiss means facing opponents which already have one or more losses, therefore their contribution to our rating will be most likely detrimental. Also, it’s possible that a number of them will drop after the second or third loss, which makes their contribution even more miserable.

Another interesting detail is that draws are generally detrimental to the first tiebreaker, almost as much as victories.

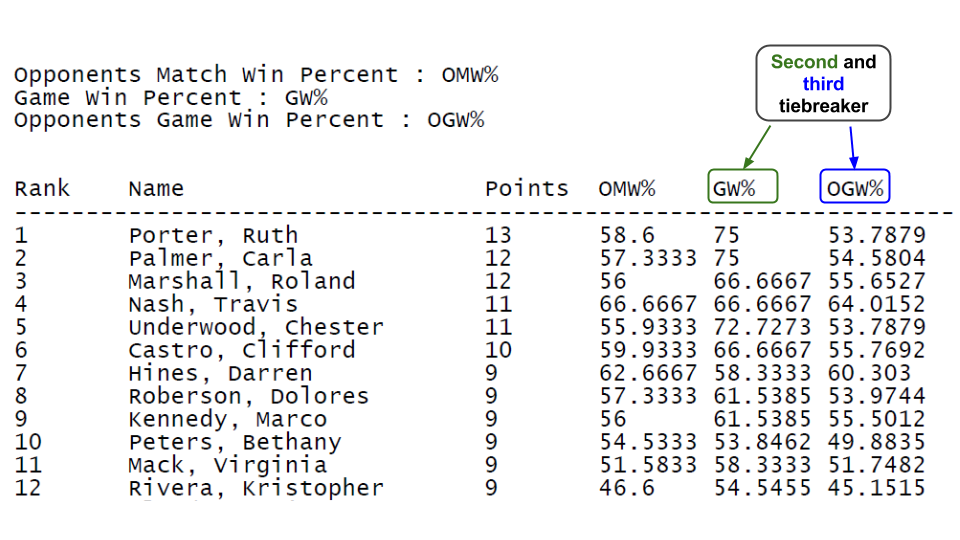
The second and third tiebreakers are based on a different principle, which is: winning 2-0 is more praiseworthy than winning 2-1. The second tiebreaker represents the percentage of games won by the player, while the third represents the percent mean of the games won by all the player’s opponents. The second tiebreaker is taken into consideration if and only if the first is identical between two players; the third, in the same way, is looked at only if both the first and the second are equal. Actually – excluding tournaments with an extremely low number of competitors – it is very unlikely that the second and third tiebreaker are anyhow influential.

Back to the first number then, which is the only one worth our interest. As we saw, losing one of the first rounds of Swiss can have devastating effects on our first tiebreaker, while losing the first match during the fifth round means that at least one opponent will be 5-0, giving us a contribution of 100% after the fifth round.

Intentionally drawing or not?

Does it exist, at the end of all these calculations, an answer to the foundamental question that stalks all the players with a X-1 score before the last round of Swiss? ID or Play?

There’s not a unique answer obviously, but there are some factors which you can take into consideration:

1. The more the tournament is big, the more your tiebreakers will tend to remain the same after the last round. If, in a 9-round tournament, all of our previous 8 opponents won, our first tiebreaker will grow barely by a 2%.
2. A draw means that your last opponent will have one less win, still having enough victories to have your same score. It can be important in a situation where a player with one more point than you, and a similar first tiebreaker, plays and loses. In this case his/her rating will likely grow a little more than yours, since your opponent of the last turn will have one less match won compared to his/her one. This is true under the absumption that your opponents of the previous rounds and his/her ones have roughly the same trend (which will be true on the long run, for statistical reasons).
3. In a situation when a player with 2 points less than you, and a similar tiebreaker, is playing to reach the same score you’d reach with an ID, his/her first tiebreaker will generally grow less than yours. Effectively, both your opponents of the last round will have one less match won (the difference between a tie and a loss is minimal, as we already saw), but since you faced an opponent with an higher score, he/she will give a better contribution to your rating. This doesn’t apply if both the opponents have the same score (one between you and the player with 2 points less than you is either paired up or down), and still goes under the absumption that previous opponents have roughly the same trend.
4. Generally speaking, the structure of the Swiss is made to make it mathematically impossible to stay out of the Top8 with a score of X-0-2 (X victories, zero losses and two ties). Besides some very rare corner cases, two players with a score of X-0-1 should be always able to ID.
5. The program which generates the pairings does not take tiebreakers into account while pairing the players. Pairings are based on points, and then random: the player with the highest tiebreaker at 12 points can be the one paired down, if the players at 12 points are an odd number.

The secrets of the Pairings

One more detail on this last point: the WER couples the players starting from the ones with the highest score. As long as it finds someone with the highest score, it pairs them randomly (without taking tiebreakers into account, as we said). When the program made all the possible pairings, he goes to the second-highest score and repeats the process: if the players with the highest score are an odd number, one of them will be paired with a player with a lower score.

When the program reaches the lower possible score, it still makes all the possible pairings, and gives a bye to the remaining player, if any.

This means that even if there are seven more players with your same score (a total of 8), you can still be paired up or down: it depends from the number of players with an higher score being odd or even.

Finally, what’s the influence of a bye on the tiebreakers? It is none. The program, while computing the average of your opponents match-winning percentages, will have one less value to consider: if you received a bye during the first round of a 6 round tournament, the program will simply mean over 5 values instead of 6. However, if you look at the standings after the first round, you’ll see the player with the bye having a tiebreaker of 100% (you’ll notice it, since all the other players with 3 points will have a tiebreaker of 33%): this is not his/her real tiebreaker, this is only a default value that is used because the program cannot compute the mean of 0 numbers.

An early bye is still beneficial for your tiebreakers though, since it means that you’ll be facing players with an higher score, with a lower risk of opponents of early rounds going 0-3-drop.

Conclusions

Tiebreakers will often be a decisive factor in determining your access to a tournament’s Top8. Knowing how it works can be important in order to decide if intentionally drawing a match or not, and more…

Asking an opponent to concede a match in a situation where your tiebreakers would allow you to enter the Top8 with a victory, while he/she couldn’t make it in any case, is a legit request; similarly, if reading the standings you realize you basically have no hope, this can make your decision to concede easier.

Clearly, you aren’t allowed to ask or offer anything in exchange for a concession, but this is hopefully something all of you already know.

Good luck to everybody

 

Based on the original article of IMJ.

 

Credits